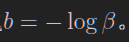第一章 随机变量

累积分布函数

观测值小于等于x的概率

\[\begin{align} F(x) &= \sum_{xi \le x} P(x_i) & \text{离散} \\ F(x) &= \int_{-\infin}^x f(x\prime)dx\prime & \text{连续} \end{align}\]

各种矩

image-20250620101956015

分位数

使$F(x) = \alpha$的x，或者说$x = F^{-1}(\alpha)$

联合概率密度分布函数

\[\iiint f(x, y) dx dy = 1\]
\[f_x(x) = \int f(x, y) dy = \int g(x | y)f_y(y) dy\]

上面这个函数称为边缘概率密度函数，显然这个函数在有两个变量的情况下只考虑一个变量

重要公式（1.32）a(x)为x的函数，x的分布知道，为f(x)，求a的分布g(a)

\[g(a) = f(x(a))\left|\frac{dx}{da}\right|\]

备注：如果函数不是单调函数，那么需要把所有反函数x(a)带进去，求完后加起来

下面这个公式是对他的推广

image-20250617130106758

1.35梅林卷集，只适用于z=xy的情况求z的概率密度函数

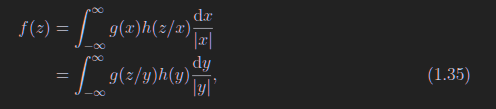
image-20250617125839950

下面只适用于z=x+y

image-20250617125953089

方差、协方差、关联系数

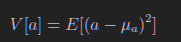
image-20250617130247004

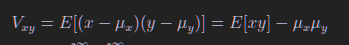
image-20250617130259011

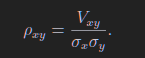
image-20250617130313512

image-20250617130500939

1.6 误差传递

image-20250617134843714

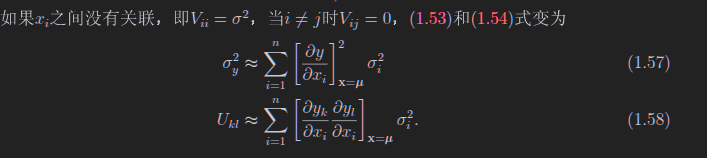
image-20250617140455063

第二章 常用分布

2.1 二项/多项分布

要么成功，要么失败

N次试验中成功n次概率、期待值、方差

\[\begin{align} f(n; N, p) &= \mathrm{C}^n_{N} p^n (1-p)^{N-n} \\ E[n] &= Np \\ V[n] &= Np(1 - p) \end{align}\]

多项分布，每一次实验的结果不止两个，每一个结果对应一个p，显然

\[\sum_i p_i = 1\]

若有N次实验，每一次试验产生一个结果，试验完成后，第一个可能结果有n1次出现，第二个有n2个，显然

\[\begin{align} \sum_i n_i &= N \\ f(n_1, ..., n_m; N; p_1, ..., p_m) &= \frac{N!}{n_1!n_2!...n_m!}p_1^{n_1}...p_m^{n_m} \end{align}\]

如果这样思考：第i个事件发生了即为成功，没有发生（发生了其他的事件）则为失败，这不就是个二项分布吗，所以第i个事件的期望和方差同上面的二项分布

2.2 泊松分布

在二项分布的极限情况，即N很大p很小，Np为一个有限值，二项分布近似为泊松分布

\[\begin{align} f(n;\nu) &= \frac{\nu^n}{n!} e^{-\nu} \\ E[n] &= \nu \\ V[n] &= \nu \end{align}\]

若$\nu$很大，则泊松分布可以近似为高斯分布

2.3 均匀分布

\[\begin{align} f(x; \alpha, \beta) &= \begin{cases} \frac{1}{\beta - \alpha} & \alpha \le x \le \beta \\ 0 & otherwise \end{cases} \\ E[x] &= \frac{1}{2} (\alpha + \beta) \\ V[x] &= \frac{1}{12} (\beta - \alpha)^2 \end{align}\]

2.4 指数分布

\[\begin{align} f(x; \alpha, \beta) &= \frac{1}{\xi}e^{-x / \xi} \\ E[x] &= \xi \\ V[x] &= \xi^2 \end{align}\]

2.5 高斯分布

\[\begin{align} f(x; \mu, \sigma^2) &= \frac{1}{\sqrt{2 \pi \sigma^2}}\exp(-\frac{(x - \mu)^2}{2 \sigma^2}) \\ E[x] &= \mu \\ V[x] &= \sigma^2 \end{align}\]

一个小定理:

\[y \sim N(\mu, \sigma^2) \Rightarrow x = \frac{y - \mu}{\sigma} \sim N(0, 1)\]

中心极限定理

如果n个独立连续随机变量，$\mu_i, \sigma^2_i$，没有说他们是什么分布，他们的和满足$\mu = \sum_i \mu_i, \sigma^2 = \sum_i \sigma^2_i$的高斯分布。

2.6 卡方分布

函数形式不想写

image-20250617154700634

\[\begin{align} E[z] &= n \\ V[z] &= 2n \end{align}\]

上面的n是自由度，若$x_i \sim N(0, 1)$，则$\sum_ix_i^2$满足自由度为N的卡方分布。所以拟合的卡方每自由度最好是1

第三章 蒙卡方法

3.2 变量变换法

想要用f(x)抽样x，

  1. 求f(x)的累积分布
  2. 求累积分布的逆函数
  3. 把均匀分布带入逆函数，即可

第四章 统计检验

4.1 假设、检验统计量、显著水平和效力

统计检验目的：看看观测的数据和预期的假设对不对的上

  • 零假设：考察中的假设
  • 备选假设：和零假设比较的
  • 简单假设：在这个假设下，概率密度函数可以直接被完全确定

  • 复杂假设：在这个假设下确定的概率密度函数有个可以变动的参数

  • 检验统计量，完全可以用原始数据来当作检验统计量，但是维度太高了，所以换一个简单的
    • 可以这么理解$t = t(\vec x)$
    • 这也是个统计量，从x算出来的或者测出来的，你不用管这个啰嗦奇葩的术语，真啰嗦啊生怕我看懂它？
    • 在假设不同的情况下，统计量的分布也不同，看下面这个b图，这个是在假设正确的情况下画出来的，也就是说真实的t分布可能不是这个样子的

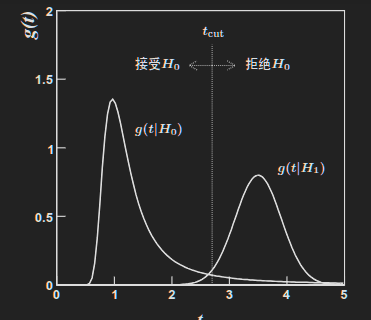
image-20250617184929190

  • 拒绝域：
    • 你看上面这个b图，如果H0正确的话，那么测出来的t处于2.7以上的位置是不是几率特别小？
    • 可以把2.7及以上的位置定义为拒绝域
    • 按照我们的假设H0，处在这个拒绝域概率很小，假设这个概率为5%吧！
    • 这个5%就叫做显著水平
    • 2.7这个位置就叫做tCut，判选条件
    • 现在来看，如果H0为真，那是不是有5%拒绝H0？，这个叫第一类误差

image-20250617191557392

  • 效力
    • 现在需要看g(t H1)了，如果H1是真的，那么t测量出来比2.7小是不是概率很低？那么2.7就是tCut了，假设这个概率为7%，这个7%为显著水平
    • 现在我们看，我们先入为主，把H0认为零假设，测出来的t也让我们接受H0,但是这个时候H1是真的，此时这个7%称为第二类误差，也就是下面这个图的beta，同时可以定义效力

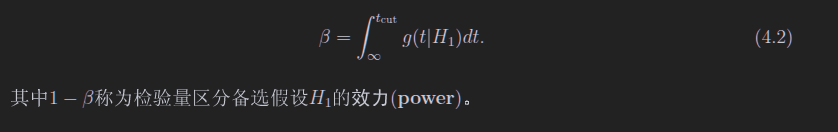
image-20250617192521252

可以看出，我们的零假设不同，这些alpha和beta的值也不同

alpha和beta都是两个分布的小脚，很好记

4.2 粒子选择的统计检验

在4.1中，把H0认为是电子，H1认为是pi，认为电子是目标，pi是背景。那么

选择效率

  • $\epsilon_e = 1 - \alpha$
  • $\epsilon_\pi = \beta$

若pi是目标，那么

$\epsilon_e = \alpha$

$\epsilon_\pi = 1 - \beta$

这玩意很好理解，就是由于tcut的原因，我们会舍去一些真正的电子和真正的pi

纯度

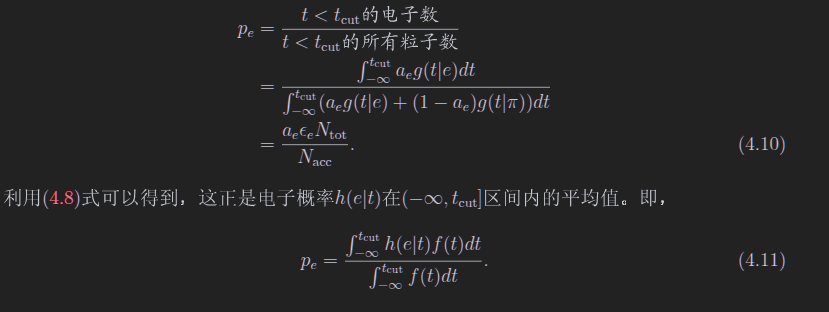
image-20250618095131113

其中

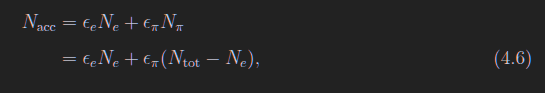
image-20250618100245471

上图中，$a_e$和$a_\pi$题目会给的

纯度需要给定tCut

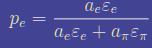
image-20250618104534447

上面的式子更好理解，你把分子分母同乘以Ntotal，Ntotal再和比率去乘，就是电子和pi的数量，这个数量在去乘以选择效率，就是在tcut下的粒子数了

4.3 4.4 奈曼皮尔逊引理选择拒绝域以及构造统计量

image-20250618111013216

说人话：信噪比最高

image-20250618111119871

就是找一个区域，信噪比高于这个给定比值

接下来干的事情是，构造统计量，并且使得统计量的概率密度函数分离最大

本章节为了简单，使用的统计量是原数据的线性函数

image-20250618190943275

显然，每一个假设可以对应一个原始数据的期望及方差，t也是，每一个假设都有一个t的方差和期望，这个思想就是：不同假设的t的期望差别很大不就行了？

同时呢，希望t的各个分布图像比较尖，也就是方差小，于是，就构建了一个统计量

image-20250618193800888

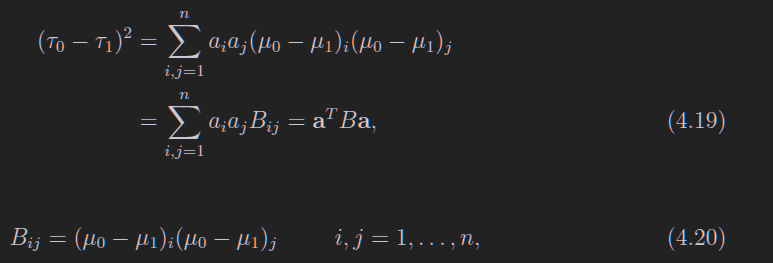
image-20250618194019526

这个B如下表述清晰一些

\[B = (\vec\mu_0 - \vec\mu_1)(\vec\mu_0 - \vec\mu_1)^T\]

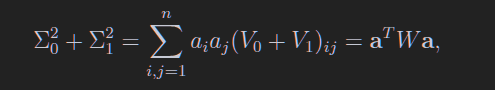
image-20250618194445825

image-20250618194606796

显然，B和W都是对称矩阵

image-20250618213957462

这个多维高斯的指数部分要记

这里用了两个性质

  1. W和V包括他们的逆矩阵是对称矩阵，所以这里没写T
  2. a是正比于那个系数的（4.23）所以本来这里有个2，被吸收进去了

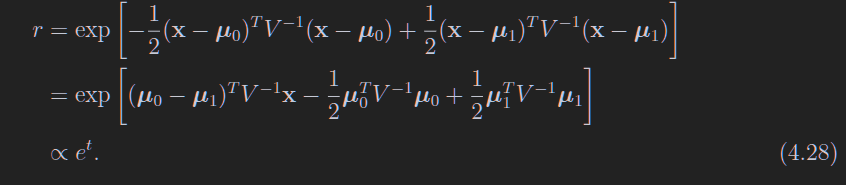
image-20250618215543865

显然，这个r是用下面的这个算出来的，但是书上写的牛头不对马嘴

\[r = \frac{f(x|H_0)}{f(x|H_1)}\]

image-20250619104208504

上式子省略了一个重要步奏，那就是选择合适的a0,使得前面的系数消失,所以这里e前面没有系数

\[\frac{\pi_1}{\pi_0} \exp[\frac{1}{2}\mu_0^T x \mu_0 - \frac{1}{2}\mu_1^Tx\mu_1 + a_0] = 1\]

如上所示

4.5 拟合优度检验

看看零假设和观测数据拟合的好不好

定义一个P，这是一个概率，简单来说，就是现在有个假设分布f(x)，然后呢我做了个实验，得到一个值，这个值与我假设分布的期望值有偏差，那现在我来看，在f(x)的分布下，测量一个新的值比现在的测量值更差的概率是多少，这个就是P

*4.7 皮尔逊卡方检验

第五章 参数估计

5.2 样本均值、方差和协方差

不奇怪但是重要的公式

image-20250619155439934

第一个是因为xi和xj独立，第二个是用的方差公式

大数弱定理

如果x的方差存在，则xbar为全平均的一致性估计量，这个看习题的5.1

样本均值

image-20250619143642224

image-20250619143856884

样本方差

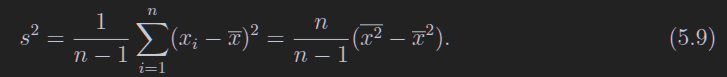
image-20250619144024037

如果均值是知道的，那么就不需要n-1了

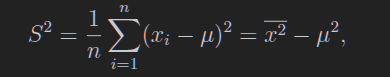
image-20250619145108139

证明步骤

用上奇怪的公式，随便证明

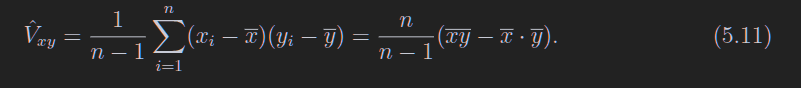
image-20250619151101668

image-20250619151151333

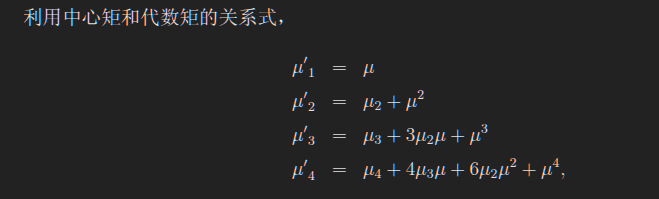
image-20250619185327165

第六章 最大似然法

很简单的一个思想，假定一个带参数的分布$f(x;\theta)$

image-20250619193746861

这个总概率最大，那么这个f不就可以尽量拟合数据的分布了吗

image-20250619193940352

怎么求最大的概率呢？直接求导就行了

image-20250619194059637

6.2 指数分布的最大似然函数

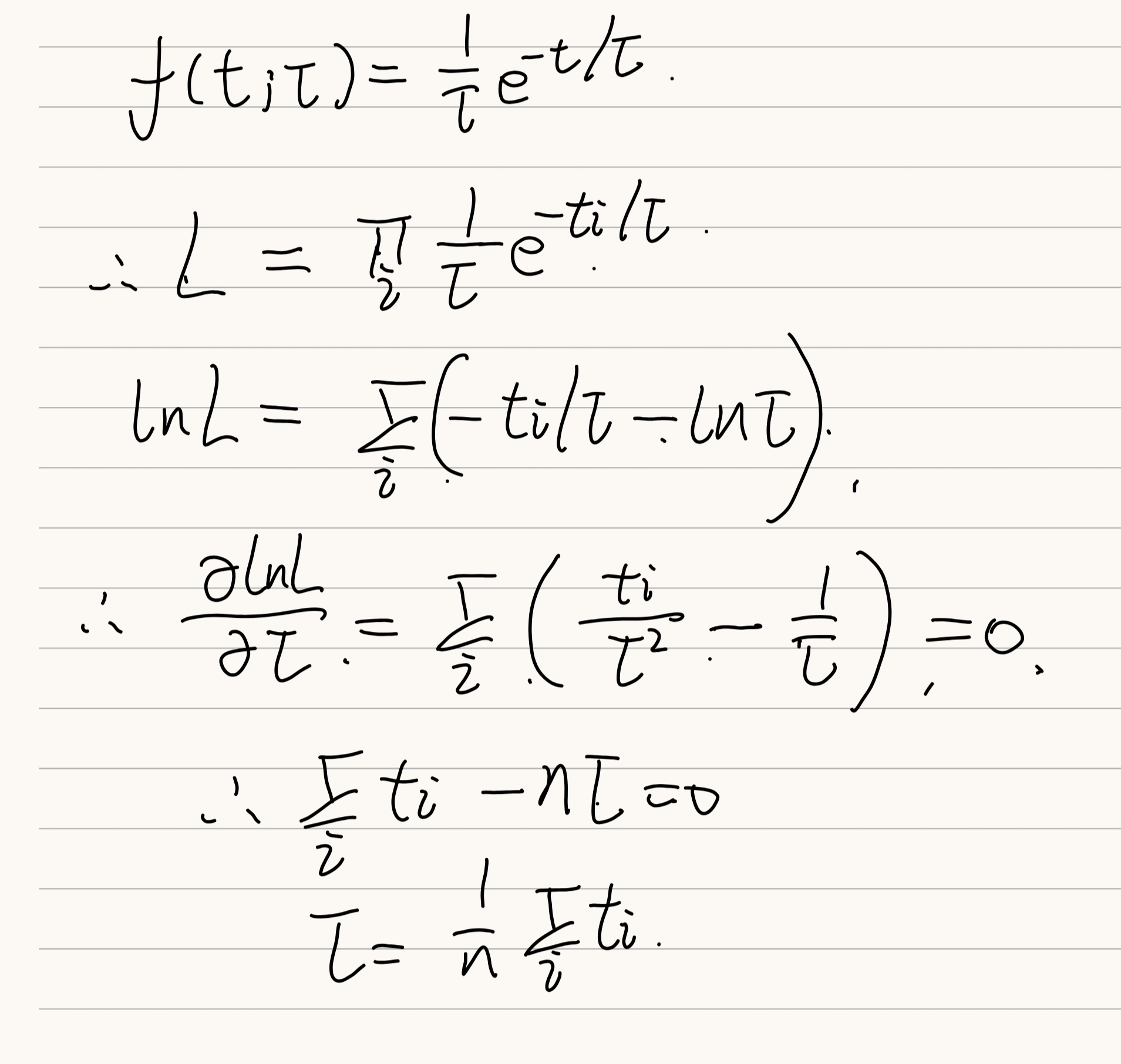
上面这个意味着，如果我想使用指数函数去拟合，那么就可以直接求个平均后往函数里面带

如果想换个变量，可以干下面的事情，只要a对theta的导数不是0,那么L对a的导数就是0,这样可以不用theta作为估计量，而换一个参数

image-20250619201704914

6.3 高斯分布的似然函数

6.6 RCF边界

方差不好计算的时候，给出一个最小值的估计

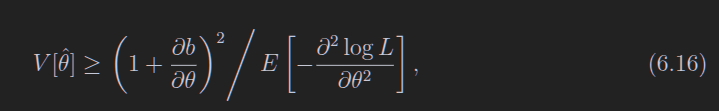
image-20250620112528471

其中

image-20250620112552471

估计量的协方差矩阵的逆

image-20250620112815552

thetai和thetaj表示两个不同的估计量，比如说高斯分布的估计量mu和sigma^2

其实这个协方差矩阵的逆长的很像RCF边界，很容易猜出他们的关系

在数据样本足够大的情况下，可以直接用最大似然估计值去约等于，而不是计算期望

image-20250620113250656

第七章 最小二乘法

之前的最大似然法是用于分布的，也就是说，横坐标是值，纵坐标是计数；这个最小二乘法是用于横坐标是值，纵坐标也是值，比如在一个位置xi测量温度得到yi。

如果我们多次测量，得到多个yi，这些yi是满足高斯分布的（大数定理）

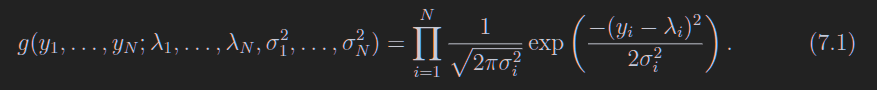
image-20250620201818110

我们在一个位置测量一次温度，那么这一个温度值yi也是满足高斯分布的，在其他位置也干一样的事情：测量一次温度，那么我们会得到多个高斯分布函数（假设每个位置的温度的真值是lambda(x)这个函数）。对于一个位置，有一个高斯分布函数，由上一章我们知道，这个函数是这个位置的似然函数。那么我们是不是可以用这些函数去求一些最大似然估计量了？

我们直接把他们全部乘起来（如7.1），忽略系数，求对数（如下）

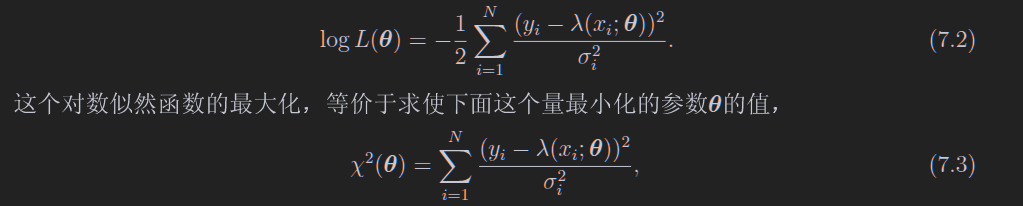
image-20250620202755329

当然，如果你的各个测量值yi之间不是独立的，用下面的式子

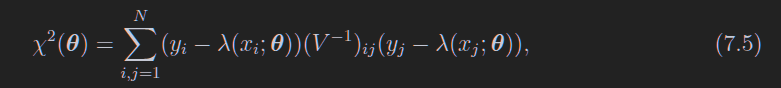
image-20250620204257845

就是高斯分布的指数部分没有2,很好记

7.2 线性最小二乘法拟合

在上面有提到一个lambda，认为lambda是参数theta的线性函数，就是这里的内容

image-20250621094052720

这里的aj相互独立就可以了

如果把7.6写成矩阵形式，就可以把卡方表达式改一个样子，如下，注意到这里的量都是矩阵

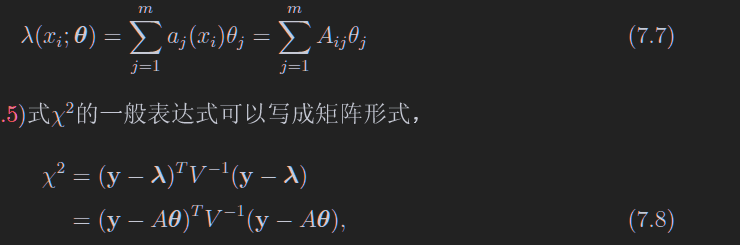
image-20250621095256008

求解这个玩意的最小值，求导就好，最后解出来如下

image-20250621100247724

这个叫最小二乘估计量

第九章 统计误差、置信区间和极限

就是教你怎么算误差，画误差棒之类的

重复样本容量相同的实验很多次，每次按相同方法构造置信区间，那么置信区间包含 θ真值的比例为 1−α−β。

image-20250622155419866

9.2 经典置信区间

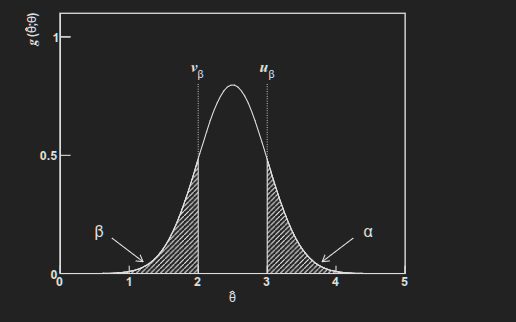
image-20250621144951044

对于这个分布g，我们可以找到一个值，使得观测到theta大于这个值的概率为alpha（图上的ubeta，图画错了，应该叫ualpha），对于概率beta同理，看图

下面的公式也写错上限了，应该是vbeta

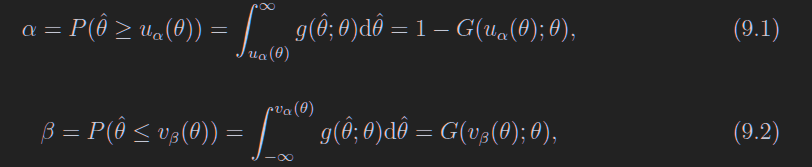
image-20250621145235767

图中没有阴影的部分被称作置信带

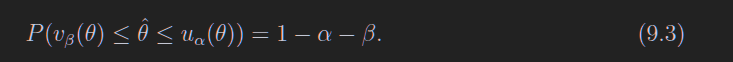
image-20250621145316435

实际上我们经常把u和v弄成反函数的样子

image-20250621150108980

image-20250621150120759

\[\begin{align} a &= a(\hat \theta) \\ b &= b(\hat \theta) \end{align}\]

[a, b]这个区间称为置信区间，1 - alpha - beta称为置信水平

image-20250622142759134

image-20250622143130567

如果你想要对称的，那么就让$\alpha = \beta = \gamma / 2$

注意这里9.3和9.8的区别，9.3是theta的估计量处于一个范围的概率，9.8是真实值处于置信区间的概率

append：高斯分布函数的分位数

image-20250621155921360

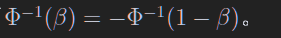
image-20250621160647430

image-20250622160530568

$a(\hat \theta)$是一个从测量值到真值的映射

9.4 泊松

image-20250622163650663

image-20250622174803948

image-20250622174824462